This post shows the step by step process of calculating the distance as the crow flies between two points using latitude and longitude of both points. I have used this calculation in logging software I have been continuously developing the last three years.

I initially wrote my logging software to record general contacts but recently enhanced to include contest logging features for VHF / UHF.

A requirement of my software is to calculate the distance between the centre of my Maidenhead locator code and the centre of the remote operators Maidenhead locator code.

This calculation will work with any latitude and longitude values, however, if you want to calculate distance between the centre of two Maidenhead locator codes you will need to firstly calculate the latitude and longitude at the centre of locator codes for start and end points.

I wrote another post to show how to calculate this using simple maths and this can be found here. Although there is nothing really complex about this calculation it does use sine, cosine, square root and to the power of. You will likely need a scientific calculator if you are doing this manually.

I’ve written this post because despite finding lots of computer programs and apps that automatically do it for you, people posting code of computer programs written to do it and information that is complicated to understand, I could not find anywhere where the process is easily explained.

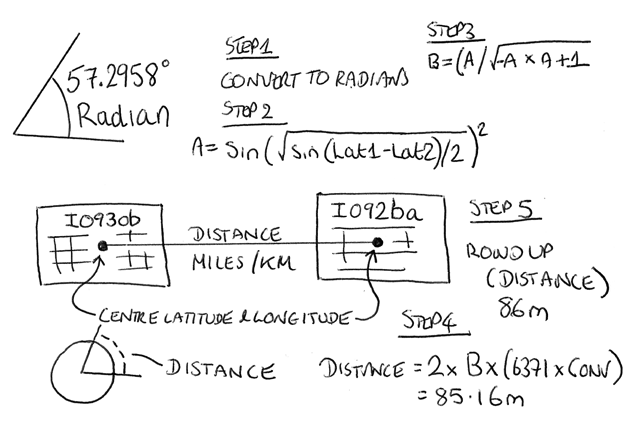
In my logging software I use five steps to calculate distance. There are some constant values (don’t change) used in this calculation; earth radius, km to miles conversion factor and Pi.

Earth radius = 6371 -Find out more about earth radius here

Km to miles conversion factor = 0.621371 – Find our more about the conversion factor here

Pi = 3.14159265359 – Find out more about Pi here

Step 1

Convert each latitude and longitude decimal degrees to radians

Latitude_1 = (53.0625 / 180) * 3.14159265359 = 0.9261153346
Longitude_1 = (-0.7916666/ 180) * 3.14159265359 = -0.01381718875

Latitude_2 = (52.020833 / 180) * 3.14159265359 = 0.9079348157
Longitude_2 = (-1.875 / 180) * 3.14159265359 = -0.03272492349

Answer_A = sin(sqrt(sin((0.9261153346 – 0.9079348157) / 2) ^ 2 + cos(0.9261153346) * cos(0.9079348157) * sin((-0.01381718875 – -0.03272492349) / 2) ^ 2))

Answer_A = 0.0107553099025581

Step 2

Answer_B = (Answer_A / sqrt(-Answer_A * Answer_A + 1))

Answer_B = 0.0107546878871914

Step 3

Distance in miles = 2 * Answer_B * (6371 * 0.621371) = 85.16 

Distance in miles = 2 * 0.0107546878871914 * (6371 * 0.621371)

Distance in miles = 85.16

Or

Distance in km = Distance in miles / 0.621371 = 137.0517

You now have a distance to an unspecified number of decimal places.

Step 4

Section 5.a. of the ‘General Rules for RSGB VHF/UHF/SHF Contests 2019’ says “Scoring will normally be at 1 point per km and commenced (part) km – i.e. 137.3km counts as 138 points. Contacts with stations in the same small locator square as your station (eg IO92AA to IO92AA) will score 1 point.”.  This suggests rounding up to the nearest km. I therefore round 137.0517 up to 138km.

RADIANS

I have included two resources that explain what radians are. The first is from Wikipedia – click here

The second is from an educational site – click here

Why not take a look at my YouTube channel here or Twitter posts here.

You can also register for my website here.

Thanks

73 de M0NWK